Tag Archives: sampling

Our tools for solving, counting and sampling

Development, Research, SAT, Tools, , ,

This post is just a bit of a recap of what we have developed over the years as part of our toolset of SAT solvers, counters, and samplers. Many of these tools depend on each other, and have taken greatly from other tools, papers, and ideas. These dependencies are too long to list here, but the list is long, probably starting somewhere around the Greek period, and goes all the way to recent work such as SharpSAT-td or B+E. My personal work stretches back to the beginning of CryptoMiniSat in 2009, and the last addition to our list is Pepin.

Overview

Firstly when I say “we” I loosely refer to the work of my colleagues and myself, often but not always part of the research group lead by Prof Kuldeep Meel. Secondly, almost all these tools depend on CryptoMiniSat, a SAT solver that I have been writing since around 2009. This is because most of these tools use DIMACS CNF as the input format and/or make use of a SAT solver, and CryptoMiniSat is excellent at reading, transforming , and solving CNFs. Thirdly, many of these tools have python interface, some connected to PySAT. Finally, all these tools are maintained by me personally, and all have a static Linux executable as part of their release, but many have a MacOS binary, and some even a Windows binary. All of them build with open source toolchains using open source libraries, and all of them are either MIT licensed or GPL licensed. There are no stale issues in their respective GitHub repositories, and most of them are fuzzed.

CryptoMiniSat

CryptoMiniSat (research paper) our SAT solver that can solve and pre- and inprocess CNFs. It is currently approx 30k+ lines of code, with a large amount of codebase dedicated to CNF transformations, which are also called “inprocessing” steps. These transformations are accessible to the outside via an API that many of the other tools take advantage of. CryptoMiniSat used to be a state-of-the-art SAT solver, and while it’s not too shabby even now, it hasn’t had the chance to shine at a SAT competition since 2020, when it came 3rd place. It’s hard to keep SAT solver competitive, there are many aspects to such an endeavor, but mostly it’s energy and time, some of which I have lately redirected into other projects, see below. Nevertheless, it’s a cornerstone of many of our tools, and e.g. large portions of ApproxMC and Arjun are in fact implemented in CryptoMiniSat, so that improvement in one tool can benefit all other tools.

Arjun

Arjun (research paper) is our tool to make CNFs easier to count with ApproxMC, our approximate counter. Arjun takes a CNF with or without a projection set, and computes a small projection set for it. What this means is that if say the question was: “How many solutions does this CNF has if we only count solutions to be distinct over variables v4, v5, and v6?”, Arjun can compute that in fact it’s sufficient to e.g. compute the solutions over variables v4 and v5, and that will be the same as the solutions over v4, v5, and v6. This can make a huge difference for large CNFs where e.g. the original projection set can be 100k variables, but Arjun can compute a projection set sometimes as small as a few hundred. Hence, Arjun is used as a preprocessor for our model counters ApproxMC and GANAK.

ApproxMC

ApproxMC (research paper) is our probabilistically approximate model counter for CNFs. This means that when e.g. ApproxMC gives a result, it gives it in a form of “The model count is between 0.9*M and 1.1*M, with a probability of 99%, and with a probability of 1%, it can be any value”. Which is very often enough for most cases of counting, and is much easier to compute than an exact count. It counts by basically halfing the solution space K times and then counts the remaining number of solutions. Then, the count is estimated to be 2^(how many times we halved)*(how many solutions remained). This halfing is done using XOR constraints, which CryptoMiniSat is very efficient at. In fact, no other state-of-the-art SAT solver can currently perform XOR reasoning other than CryptoMiniSat.

UniGen

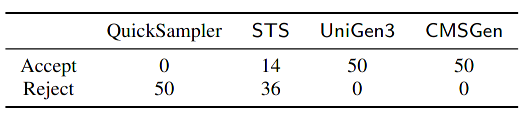
UniGen (research paper) is an approximate probabilistic uniform sample generator for CNFs. Basically, it generates samples that are probabilistically approximately uniform. This can be hepful for example if you want to generate test cases for a problem, and you need the samples to be almost uniform. It uses ApproxMC to first count and then the same idea as ApproxMC to sample: add as many XORs as needed to half the solution space, and then take K random elements from the remaining (small) set of solutions. These will be the samples returned. Notice that UniGen depends on ApproxMC for counting, Arjun for projection minimization, and CryptoMiniSat for the heavy-lifting of solution/UNSAT finding.

GANAK

GANAK (research paper, binary) is our probabilistic exact model counter. In other words, it returns a solution such as “This CNF has 847365 solutions, with a probability of 99.99%, and with 0.01% probability, any other value”. GANAK is based on SharpSAT and some parts of SharpSAT-td and GPMC. In its currently released form, it is in its infancy, and while usable, it needs e.g. Arjun to be ran on the CNF before, and while competitive, its ease-of-use could be improved. Vast improvements are in the works, though, and hopefully things will be better for the next Model Counting Competition.

CMSGen

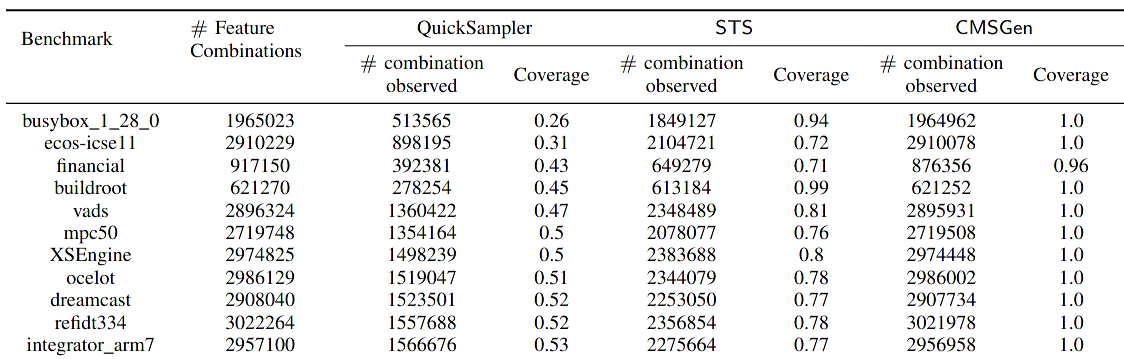
CMSGen (research paper) is our fast, weighted, uniform-like sampler, which means it tries to give uniform samples the best it can, but it provides no guarantees for its correctness. While it provides no guarantees, it is surprisingly good at generating uniform samples. While these samples cannot be trusted in scenarios where the samples must be uniform, they are very effective in scenarios where a less-than-uniform sample will only degrade the performance of a system. For example, they are great at refining machine learning models, where the samples are taken uniformly at random from the area of input where the ML model performs poorly, to further train (i.e. refine) the model on inputs where it is performing poorly. Here, if the sample is not uniform, it will only slow down the learning, but not make it incorrect. However, generating provably uniform samples in such scenarios may be prohibitively expensive. CMSGen is derived from CryptoMiniSat, but does not import it as a library.

Bosphorus

Bosphorus (research paper) is our ANF solver, where ANF stands for Algebraic Normal Form. It’s a format used widely in cryptography to describe constraints over a finite field via multivariate polynomials over a the field of GF(2). Essentially, it’s equations such as “a XOR b XOR (b AND c) XOR true = false” where a,b,c are booleans. These allow some problems to be expressed in a very compact way and solving them can often be tantamount to breaking a cryptographic primitive such as a symmetric cipher. Bosphorus takes such a set of polynomials as input and either tries to simplify them via a set of inprocessing steps and SAT solving, and/or tries to solve them via translation to a SAT problem. It can output an equivalent CNF, too, that can e.g. be counted via GANAK, which will give the count of solutions to the original ANF. In this sense, Bosphorus is a bridge from ANF into our set of CNF tools above, allowing cryptographers to make use of the wide array of tools we have developed for solving, counting, and sampling CNFs.

Pepin

Pepin (research paper) is our probabilistically approximate DNF counter. DNF is basically the reverse of CNF — it’s trivial to ascertain if there is a solution, but it’s very hard to know if all solutions are present. However, it is actually extremely fast to probabilistically approximate how many solutions a DNF has. Pepin does exactly that. It’s one of the very few tools we have that doesn’t depend on CryptoMiniSat, as it deals with DNFs, and not CNFs. It basically blows all other such approximate counters out of the water, and of course its speed is basically incomparable to that of exact counters. If you need to count a DNF formula, and you don’t need an exact result, Pepin is a great tool of choice.

Conclusions

My personal philosophy has been that if a tool is not easily accessible (e.g. having to email the authors) and has no support, it essentially doesn’t exist. Hence, I try my best to keep the tools I feel responsible for accessible and well-supported. In fact, this runs so deep, that e.g. CryptoMiniSat uses the symmetry breaking tool BreakID, and so I made that tool into a robust library, which is now being packaged by Fedora, because it’s needed by CryptoMiniSat. In other words, I am pulling other people’s tools into the “maintained and supported” list of projects that I work with, because I want to make use of them (e.g. BreakID now builds on Linux, MacOS, and Windows). I did the same with e.g. the Louvain Community library, which had a few oddities/issues I wanted to fix.

Another oddity of mine is that I try my best to make our tools make sense to the user, work as intended, give meaningful (error) messages, and good help pages. For example, none of the tools I develop call subprocesses that make it hard to stop a computation, and none use a random number seed that can lead to reproducibility issues. While I am aware that working tools are sometimes less respected than a highly cited research paper, and so in some sense I am investing my time in a slightly suboptimal way, I still feel obliged to make sure the tax money spent on my academic salary gives something tangible back to the people who pay for it.

Checking Uniform-Like Samplers

SAT, SMT, Tools, ,

Uniform sampling is pretty simple: there are a set of solutions to a set of equations, and I want you to give me N solutions uniformly at random. Say, I have a set of equations that only has the solutions x=1…6, and I ask you to give me solutions uniformly at random. In this case, if the system is not cheating, it should give me solutions exactly like a random dice would give: 1..6, each with the same probability of 1/6. Now, if you give me nothing but 1’s I’d be slightly confused, and eventually would think you may be trying to cheat.

Uniformity is useful not only in gambling, but also e.g. if you want to make sure to cover a good chunk of the potential states in a system. Say, your equations describe how a program can run. Now, uniform solutions to these equations will be examples of the state space of your program. If you want to check that your system is in most cases doing the right thing, you can ask for uniform solutions at random and check the states for inconsistencies or unexpected behaviors.

Uniform Sampling of CNFs

One type of equations that is quite popular is to have all variables boolean (i.e. True/False), and equations being nothing but an “AND of ORs”, i.e. something like: “(a OR b) AND (b OR c OR d) AND (-f OR -g)”. These types of equations, also known as CNF, can express quite complicate things, e.g. (parts of) computer programs, logical circuits (e.g. parts of CPUs), and more. What’s nice about CNF is that there are many different tools to convert your problem language into CNF.

Given CNF as the intermediate language, all you need to do is run a uniform sampler on the CNF, and interpret the samples given your transformation. For example, you could translate your Ethereum cryptocurrency contract into QF_BV logic and blast that to CNF using e.g. the STP solver. Then you can get uniform random examples of the execution of your cryptocurrency contract using e.g. UniGen.

There are many different samplers for CNFs, and they mostly fall into two categories: ones that give guarantees and are hence truly uniform, and ones that don’t give guarantees and therefore fall into what we’ll call uniform-like samplers. These latter samplers tend to be significantly faster than truly uniform samplers, however, they can, and sometimes do, give non-uniform samples. I personally help maintain one truly uniform sampler, UniGen (PDF), and one uniform-like sampler, CMSGen (PDF). Other popular truly uniform samplers include KUS (PDF) and SPUR (PDF).

Catching Uniform-Like Samplers: Barbarik

If I give you a sampler and ask you to tell me if it’s truly uniform or simply uniform-like, what should you do? How should we distinguish one from the other, without looking into the internals of the system? It turns out that this is not a simple question to answer. It is very reasonable to assume that there are e.g. 2^200 solutions, so e.g. trying to prove that a sampler is uniform by saying that it should only output the same sample twice rarely is not really meaningful. In this latter case, you’d need to get approx 2^100 samples from a truly uniform sampler before it will likely give two colliding samples. While a uniform-like sampler may collide at e.g. only 2^60 (i.e. a trillion times earlier), that’s still a lot of computation, and only a single data point.

Doing this efficiently is the question that was on the minds of the authors of Barbarik. Basically, their idea was the following: take a CNF, remove all solutions but two, and blow up these two solutions into equally many solutions each. Say, you find two solutions to a CNF, one BLUE and one RED. Barbarik will take BLUE, make 100 blue balls out of it, and take RED, and make 100 red balls out of it. Then, it will give the CNF with the 200 solutions, half blue, half red, to the sampler under test. Then it asks the sampler to give it a bunch of balls. We of course expect approx 50%-50% red-blue distribution of balls from a truly uniform sampler.

Barbarik fails a solver if it is gives a distribution too far away from the 50%-50% we’d expect. Barbarik runs this check many times, with different example blue/red solutions that are “blown up” to multiple solutions. Given different base CNFs, and many tries, it is possible to differentiate the good from the bad… most of the time:

If you take a look at the table above, QuickSampler and STS, both uniform-like samplers, are rejected by Barbarik given 50 different CNFs. In contrast, UniGen survives all 50 tests with flying colors. Notice, however, that CMGen also survived all tests.

The Birth of CMSGen

When Barbarik was being created, I was fortunate enough to be present, and so I decided to tweak my SAT solver, CryptoMiniSat purely using command-line parameters, until Barbarik could not distinguish it from a truly uniform sampler. This, in my view, showcased how extremely important a test system was: I actually had a bug in CryptoMiniSat’s randomization that Barbarik clearly showed and I had to fix to get higher quality samples. We called the resulting uniform-like sampler CMSGen, and it was used in the function synthesis tool Manthan (PDF), that blew all other function synthesis system out of the water, thanks to its innovative design and access to high quality, fast samples from CMSGen:

Notice that within 200 seconds Manthan outperformed all other function synthesis systems, even if we give the other system 7000 seconds to work with. If you are interested in the details of this crazy improvement over previous state-of-the-art, check out the slides here or the video here (these are all work of my coworkers, I am not an author).

While CMSGen was clearly fast and powerful, it bothered me endlessly that Barbarik couldn’t demonstrate that it wasn’t a truly uniform sampler. This eventually lead to the development of ScalBarbarik.

The Birth of ScalBarbarik

Since CMSGen passed all the tests of Barbarik, we had to come up with a new trick to distinguish it from truly uniform samplers. ScalBarbarik‘s (PDF) underlying system is still the same as Barbarik: we take a CNF, take 2 samples from it, and blow both of these samples up to a certain number. However, how we blow them up is where the trick lies. Before, they were both blown up the same way into solutions that are equally easy/hard to find. However, this time around, we’ll make one of the solution types much harder to find than the other. For this, we’ll use Vegard Nossum’s SHA-1 CNF generator (PDF) to force the system to reverse a partial, reduced-round SHA-1 hash, with some fixed inputs & outputs. This allows us to both change the complexity of the problem and the number of solutions to it rather easily.

While one set of solutions will be hard to find, the other ones will be trivial to find — if one special variable is set to TRUE, the finding a set of solutions is trivial But when it’s set to FALSE, the system has to reverse a reduce-round SHA-1. The logic behind this is that the uniform-like systems will likely be finding the easy solutions with much higher probability than the hard solutions, so they will sample much more unevenly. Indeed that’s the case:

Note that as the hardness parameter is increased, CMSGen is rejected more and more often, and eventually it’s rejected for all CNFs. Also interesting to note is that QuickSampler and STS get both rejected, as before, but this time around, STS gets rejected for all 50 CNFs, rather than for only 36 out of 50. In other words, ScalBarbarik is overall a stronger/better distinguisher.

Conclusions

With the birth of Barbarik, a set of uniform-like testers were shown to be less than ideal, and a new, more robust near-uniform sampler was born, CMSGen. But as a the gauntlet has been throw down by CMSGen, a new tool emerged, ScalBarbarik, to help find the non-truly uniform samplers. With this cycle in mind, I hope that new, more elaborate, and higher-quality uniform-like samplers will emerge that will be able to beat ScalBarbarik at its own game, improving the quality of the sampling while maintaining the speed advantage that uniform-like samplers enjoy over truly uniform samplers. With better uniform-like sampling tools, hopefully we’ll be able to make headway in automated test case generation (imagine having it as part of all development IDEs), higher performance function synthesis, and hopefully even more diverse areas of interest for the general public.

CMSGen, a Fast Uniform-Like Sampler

Research, SAT, Tools,

Uniform sampling is a problem where you are given a solution space and you have to present solutions uniformly, at random. In some cases, this is quite simple, say, for the lotto. Just pick 5 random numbers from a box and we are done! For the lotto the solution space is very easy to generate. However, when there are constraints on the solution space, it starts to get tricky.

Let’s say that I have a function I want to test, but the input to the function has some real-world constraints like e.g. the 1st parameter must be larger than the second, the 2nd parameter must be divisible by the 3rd etc. If I want to test that this function operates correctly, one way to do it is to generate 100 uniformly random inputs that don’t violate any of the constraints, run the function, and see if all is OK. For this, I need a fast way of generating uniform samples given the constraints on the solution space.

Sampler speed vs. accuracy

There have been many samplers proposed in the literature. I personally have worked on one called UniGen, a guaranteed approximate probabilistic sampler, meaning that it’ll give approximately uniform samples most of the time, and we have a proof to back this up. It’s a great sampler and will work very fast on many instances. However, for really complex solution spaces, it can have trouble. Say, you want to generate interesting test inputs for your deep learning algorithm. Deep neural networks tend to be extremely complex when translated to binary constraints, so UniGen will likely not be fast enough. It would give very good quality samples (i.e. properly uniform samples), but if it’s too slow, we may want to exchange quality of samples for speed of generation.

There are two well-known samplers that are supposed to generate uniform samples on complex solution spaces, QuickSampler (code), and STS (code), but give no guarantees, let’s call these “uniform-like” samplers. Unfortunately, the paper by Chakraborty et al and its resulting code Barbarik showed that these uniform-like samplers are highly non-uniform. Barbarik is a pretty neat idea that basically constructs solution spaces with known solution distributions and then asks the sampler to generate uniform samples. Knowing the solution space, Barbarik can then verify how non-uniform the sampler is. Imagine having a box with 1000 balls, half of them blue and the other half green. Now if I ask the sampler to give me 50 balls at random, and all of them are green, I’d be a bit surprised to say the least. It’d be like the 5-lottery having the same numbers 3 times in a row. Possible, but… not very likely. If I do this experiment 100 times, and I always get 50 green balls, it’s fair to conclude that the sampler is not uniform.

Our new uniform-like sampler, CMSGen

Given an effective tester, Barbarik, we (Priyanka Golia, Sourav Chakraborty, Kuldeep S. Meel, and myself) thought perhaps we can follow the nowadays very successful test-driven development (TDD) methodology. All we have to do is to make our sampler pass the test of Barbarik, while being at least as fast as STS/QuickSampler, and we’ll be good to go. In fact, given Barbarik, it only took about a week of playing around with CryptoMiniSat’s options to beat both STS and QuickSampler in both accuracy and speed. This speaks volumes to how important it is to have a robust, reliable, and fast testing framework that can give immediate feedback about the quality of samples generated.

Our new uniform-like sampler, based on CryptoMiniSat, is called CMSGen (research paper here), and effectively takes CyrptoMiniSat and applies the following set of changes, through pre-set command line options:

  • Pick polarities at random. Normally, SAT solvers use polarity caching scheme, but of course we want uniform samples over all the search space, so we need to pick polarities at random.
  • Branch on variables at random. Normally, SAT solver branch on variables that will most likely lead to a conflict to maximize search efficiency (the VSIDS heuristic). However, we want to explore the solution space as evenly as possible, and so we want to approach the solution space from as many angles as possible. If you think about the search space as an N-dimensional binary cube, then we are trying to approach this cube as any ways as possible.
  • Turn off all pre- and inprocessing. Pre and inprocessing in SAT solvers are used to minimize the instance, transforming it into something easier to solve, e.g. through Bounded Variable Elimination. We later reconstruct a viable solution based on the solution to the transformed instance. However, the transformed instance may (and often will!) have a very different solution space. We cannot have that, so we must turn this off. To be fair, some pre- and inprocessing could be left intact, e.g. subsumption and self-subsuming elimination, perhaps a future paper :)
  • Restart at static intervals. Restarts are nowadays often dynamic in modern SAT solvers, or even if not dynamic, then follow a non-regular pattern. However, that could disturb how we find solution. Imagine, let’s say that solutions with variable A set to TRUE are very easy to find, but solutions with FALSE are very hard to find. What will happen? Well, in restarts where A was randomly set to TRUE, we’ll always quickly find a solution and output it. But for restarts when A was randomly set to FALSE, the system would struggle to find a solution, and after some conflicts, it will simply restart into a status where hopefully A is set to TRUE, and it can find a solution again. It is quite clear to see that this will lead to serious issues with sampling quality. Hence, we set an adjustable but static restart interval of 100 conflicts, with higher values typically leading to more uniform samples.

Performance of CMSGen

Performance of the system is on the ridiculous scale in comparison with other samplers:

When it comes to 2-wise coverage, i.e. the quality of samples, the data speaks for itself (note, UniGen is missing here because it was too slow):

Note that between STS and QuickSampler, STS is both the more uniform sampler, but also the slower one. CMSGen overcomes this limitation: it’s both faster than QuickSampler, and more uniform than STS.

And of course, the Barbarik tester gives “Accept” on CMSGen much more often than on STS or QuickSampler:

Conclusion

If you need non-guaranteed uniform but fast sampling, I’d go and try out CMSGen. It’s really a completely different beast. It’s not a guaranteed uniform sampler, but it’s incredibly effective. In fact, it’s so effective and works so well, it took me a full year to figure out how best to generate problems for it where it wouldn’t be uniform. But that’s another paper, and another blog post! In the meantime, the sampler is here, go check it out!