Category Archives: SMT

On SAT/SMT Model Counting

Docs/Faqs, SAT, SMT

I have recently had a few discussions with people who wanted to do some form of model counting, and I decided to put my thoughts about this problem into a single blog post, hopefully bringing some light to this area. Firstly, when talking about model counting, it’s very important to think through what one actually needs to achieve. When people talk about a model, they often mean a solution to a problem, described as a set of constraints over either purely boolean variables (so-called propositional model counting) expressed in so-called CNF, or over higher-level constraints, often expressed in SMT-LIB format.

Let’s look at a CNF example:

c this is a comment
c below line means there are 5 boolean variables and 2 constraints
p cnf 5 2
1 -2 0
1 -2 3 0

The above CNF has 5 boolean variables and 2 constraints: “v1 or (not v2) = true”, and “v1 or (not v2) or v3 = true”. In this case, if “v1 or (not v2) = true” is satisfied, the other constraint is also satisfied. So we effectively only have to satisfy the “v1 or -v2” constraint. There are 3 solutions over the variables v1 and v2 to this constraint: (1, 0), (1, 1), and (0,0). For variables v3, v4, and v5 we can choose anything. So there are a total of 3*2^3 = 24 solutions to this CNF.

Let’s look at an SMT problem:

(set-logic QF_BV) ; Set the logic to Quantifier-Free BitVectors
(declare-fun bv () (_ BitVec 8)) ; Declare an 8-bit value
(assert (not (= bv #x00))) ; Assert that 'bv' is not equal to zero

In this SMT-LIB problem, we declared that the logic we will be using is the so-called quantifier-free bitvector logic, which basically gives you access to fixed-width variables such as uint8_t, and of course all the logical and fixed-bit bitwector operators such as modulo addition, division, subtraction, etc. In this particular case, we declared an 8-bit variable and banned it from being 0, so this problem has 2^8-1 solutions, i.e. 255.

Whichever format is being used, “counting” of solutions is something that may sound trivial (it’s just a number!), but once we get a bit more fiddly, it turns out that we can do many things that are actually easier, or even harder, than just counting, even though they sound very close to, or are even synonymous with, counting :

  • Figuring out if there is at least one solution. This is more appropriately called satisfiability checking. This is significantly easier than any notion of counting listed below. However, even this can be challenging. Typically, in the SMT/SAT competition, this is the so-called SMT single query track or the SAT competition Main Track. All SAT and SMT solvers such as kissat or cvc5 can run this kind of task.
  • Next up in complexity is to figure out if there is exactly one solution. This is actually very close to satisfiability checking, and requires only two so-called “incremental calls” to the SMT/SAT solver. I have seen this question pop up a lot in zero-knowledge (ZK) circuit correctness. What is needed is to run the query as per the above, but then add a constraint that bans the solution that is output by the solver, and ask the system to be solved again. If the solver outputs UNSAT, i.e. unsatisfiable, then we know there are no more solutions, and we are happy with the result. If not, it gives us another solution, which is a witness that there are at least two solutions. These queries are answered by so-called incremental SMT solvers (SMT competition track here), or incremental SAT solvers (incremental SAT competition track here). Almost all SAT and SMT solvers can work incrementally, for example cvc5 or z3. Most SAT solvers work incrementally, too, but e.g. kissat does not, and you need to use CaDiCaL instead.
  • Next up in complexity is to approximately count the solutions. Here, we are not interested that there are exactly, say, 87231214 solutions, instead, we are happy to know that there are approx 2^26 solutions. This is often good enough, in case one wants to e.g. figure out probabilities. There are very few such systems available, for SMT there is csb, and for SAT there is ApproxMC. For the special case of approximate DNF counting, I’d recommend pepin.
  • Next up in the complexity is exactly counting the solutions. Here, we want to know how many solutions there are, exactly, and we really-really need the exact number. There are few solutions to doing this over SMT, but doing this over SAT is quite developed. For SMT, I would recommend following the csb approach, and running Ganak on the blasted SAT formula instead of ApproxMC, and for SAT, there is the annual model counting competition, where Ganak won every single category this year, so I’d recommend Ganak.
  • Next up is model enumeration where it’s not enough to count the solutions, but we need a way to compactly represent and store them all. This of course requires quite a bit of disk space, as there could be e.g. 2^100 solutions, and representing them all, even in a very compact format with lots of smart ideas can take a lot of space — but not necessarily exponential amount. Currently, there is no such system for SMT, and my understanding is that only the d4 model counter can do this on SAT/CNF problems, thanks to its proof checking system, in part thanks to Randal Byrant. Once Ganak can output a proof, it will also be able to do this.

All in all, there is a very large gap between “find if there is exactly one solution” and “enumerate all solutions” — even though I have seen these two notions being mixed up a few times. The first might take only a few seconds to solve, while the other might not even be feasible, because compactly representing all solutions may be too expensive in terms of space (and that’s not even discussing time).

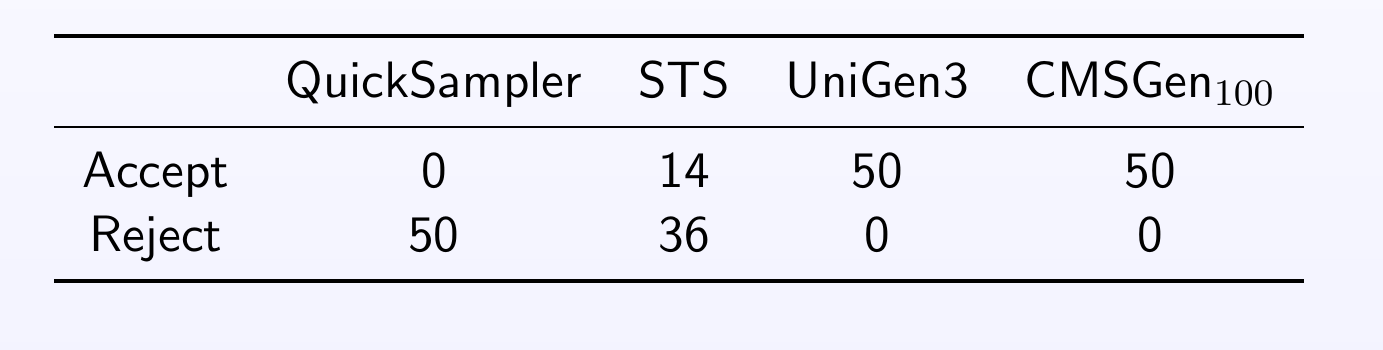
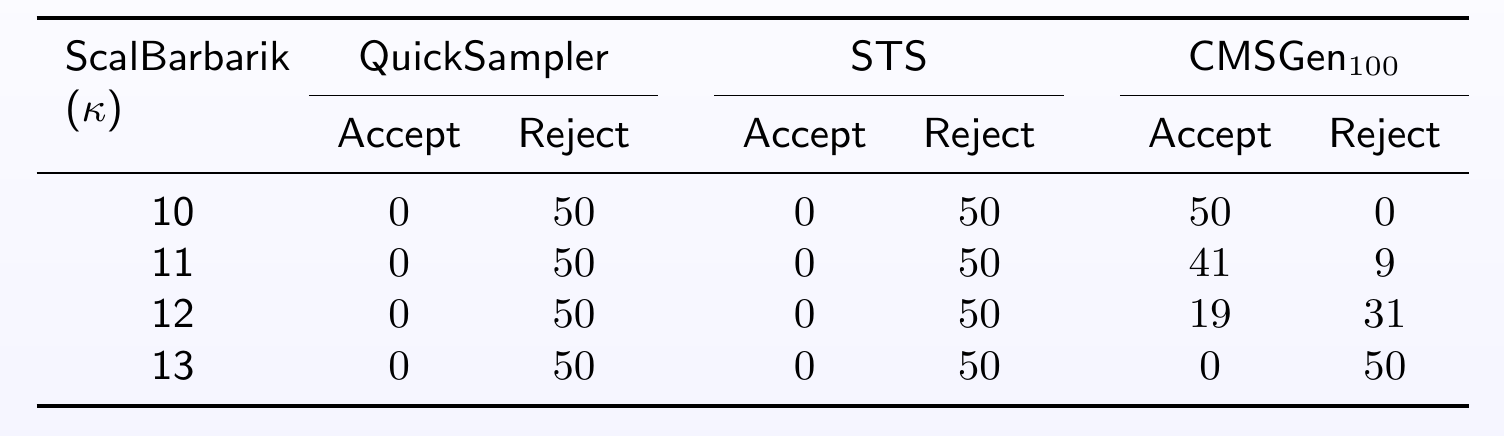
One aspect to keep in mind is that often, one does not need all solutions. For example, if one only wants to find a good set of example solutions, then it is possible to use uniform-like samplers, that give a “somewhat uniform” set of example solutions from the solution space (without guarantees of uniformity). A good tool for this is cmsgen for CNF/SAT problems. If one needs a guaranteed uniform set of samples (to be exact, a probabilistically approximately uniform sample), then unigen is the way to go. Obviously, it’s quite easy to find a uniform sample once we have an enumeration of all solutions — simply pick a random one from the whole set — but that’s way more expensive than running unigen.

While all of the above is about counting, it’s often the case that one wants to optimize for something within the solution space. Basically, we have some kind of objective function that we want to optimize for (e.g. maximize profit, minimize loss) , and so we are looking for a solution that maximizes/minimizes some property. Of course, once we have done model enumeration, it’s quite easy to do this — simply run the objective function on all solutions, and pick the best! But that’s really hard. Instead, one can formulate the problem as a so-called MaxSAT or an SMT problem with an objective function. These systems run some really smart algorithms to significantly cut down search time, and even often keep a “best so far” solution around, so we can early-abort them and still get some kind of “best so far” solution.

All in all, it’s extremely important to figure out what one actually needs, because there are vast gaps in complexity between the problems (and corresponding algorithms) above. Even between something like approximate and exact counting, the gap is gigantic, as there are huge swaths of problems that are almost trivial to count approximately, but essentially impossible to exactly count with current technology:

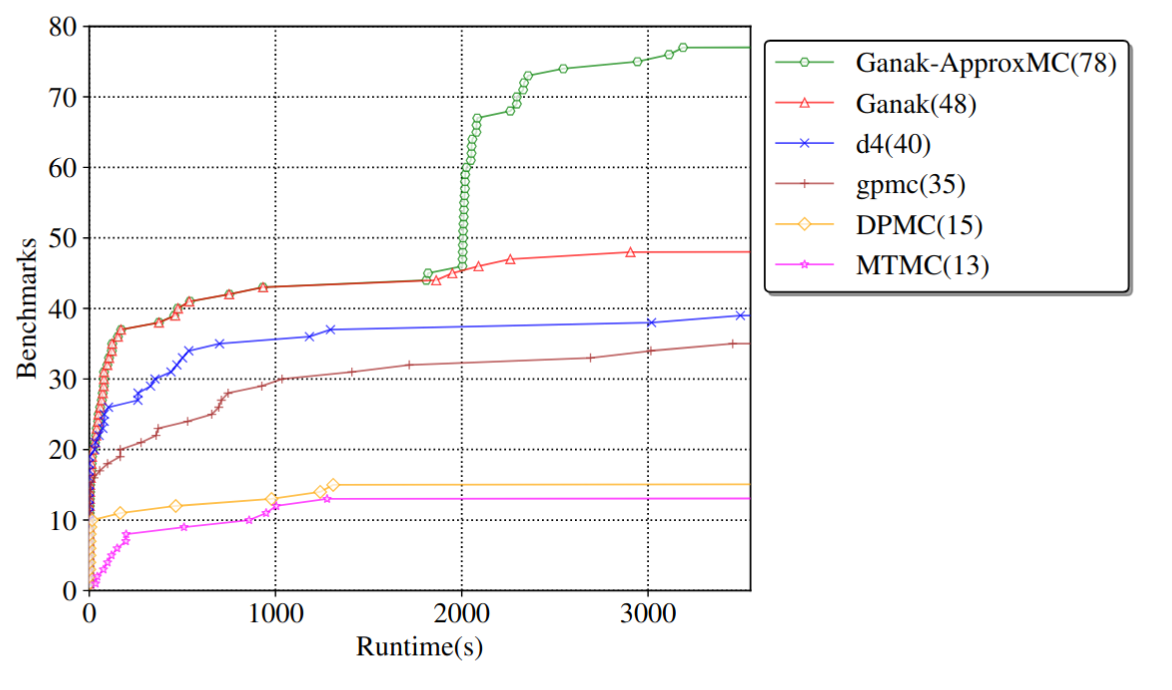
Here, the green line is a tool that changes its behaviour from exact to approximate model counting after 1800 seconds of solving, and the number of solved instances jumps significantly. Notice that the red line, the original system it runs for 1800s, is the best in class here, by a wide margin, and still the approximate counting that Ganak+ApprocMC switches into shows a massive difference.

Checking Uniform-Like Samplers

SAT, SMT, Tools, ,

Uniform sampling is pretty simple: there are a set of solutions to a set of equations, and I want you to give me N solutions uniformly at random. Say, I have a set of equations that only has the solutions x=1…6, and I ask you to give me solutions uniformly at random. In this case, if the system is not cheating, it should give me solutions exactly like a random dice would give: 1..6, each with the same probability of 1/6. Now, if you give me nothing but 1’s I’d be slightly confused, and eventually would think you may be trying to cheat.

Uniformity is useful not only in gambling, but also e.g. if you want to make sure to cover a good chunk of the potential states in a system. Say, your equations describe how a program can run. Now, uniform solutions to these equations will be examples of the state space of your program. If you want to check that your system is in most cases doing the right thing, you can ask for uniform solutions at random and check the states for inconsistencies or unexpected behaviors.

Uniform Sampling of CNFs

One type of equations that is quite popular is to have all variables boolean (i.e. True/False), and equations being nothing but an “AND of ORs”, i.e. something like: “(a OR b) AND (b OR c OR d) AND (-f OR -g)”. These types of equations, also known as CNF, can express quite complicate things, e.g. (parts of) computer programs, logical circuits (e.g. parts of CPUs), and more. What’s nice about CNF is that there are many different tools to convert your problem language into CNF.

Given CNF as the intermediate language, all you need to do is run a uniform sampler on the CNF, and interpret the samples given your transformation. For example, you could translate your Ethereum cryptocurrency contract into QF_BV logic and blast that to CNF using e.g. the STP solver. Then you can get uniform random examples of the execution of your cryptocurrency contract using e.g. UniGen.

There are many different samplers for CNFs, and they mostly fall into two categories: ones that give guarantees and are hence truly uniform, and ones that don’t give guarantees and therefore fall into what we’ll call uniform-like samplers. These latter samplers tend to be significantly faster than truly uniform samplers, however, they can, and sometimes do, give non-uniform samples. I personally help maintain one truly uniform sampler, UniGen (PDF), and one uniform-like sampler, CMSGen (PDF). Other popular truly uniform samplers include KUS (PDF) and SPUR (PDF).

Catching Uniform-Like Samplers: Barbarik

If I give you a sampler and ask you to tell me if it’s truly uniform or simply uniform-like, what should you do? How should we distinguish one from the other, without looking into the internals of the system? It turns out that this is not a simple question to answer. It is very reasonable to assume that there are e.g. 2^200 solutions, so e.g. trying to prove that a sampler is uniform by saying that it should only output the same sample twice rarely is not really meaningful. In this latter case, you’d need to get approx 2^100 samples from a truly uniform sampler before it will likely give two colliding samples. While a uniform-like sampler may collide at e.g. only 2^60 (i.e. a trillion times earlier), that’s still a lot of computation, and only a single data point.

Doing this efficiently is the question that was on the minds of the authors of Barbarik. Basically, their idea was the following: take a CNF, remove all solutions but two, and blow up these two solutions into equally many solutions each. Say, you find two solutions to a CNF, one BLUE and one RED. Barbarik will take BLUE, make 100 blue balls out of it, and take RED, and make 100 red balls out of it. Then, it will give the CNF with the 200 solutions, half blue, half red, to the sampler under test. Then it asks the sampler to give it a bunch of balls. We of course expect approx 50%-50% red-blue distribution of balls from a truly uniform sampler.

Barbarik fails a solver if it is gives a distribution too far away from the 50%-50% we’d expect. Barbarik runs this check many times, with different example blue/red solutions that are “blown up” to multiple solutions. Given different base CNFs, and many tries, it is possible to differentiate the good from the bad… most of the time:

If you take a look at the table above, QuickSampler and STS, both uniform-like samplers, are rejected by Barbarik given 50 different CNFs. In contrast, UniGen survives all 50 tests with flying colors. Notice, however, that CMGen also survived all tests.

The Birth of CMSGen

When Barbarik was being created, I was fortunate enough to be present, and so I decided to tweak my SAT solver, CryptoMiniSat purely using command-line parameters, until Barbarik could not distinguish it from a truly uniform sampler. This, in my view, showcased how extremely important a test system was: I actually had a bug in CryptoMiniSat’s randomization that Barbarik clearly showed and I had to fix to get higher quality samples. We called the resulting uniform-like sampler CMSGen, and it was used in the function synthesis tool Manthan (PDF), that blew all other function synthesis system out of the water, thanks to its innovative design and access to high quality, fast samples from CMSGen:

Notice that within 200 seconds Manthan outperformed all other function synthesis systems, even if we give the other system 7000 seconds to work with. If you are interested in the details of this crazy improvement over previous state-of-the-art, check out the slides here or the video here (these are all work of my coworkers, I am not an author).

While CMSGen was clearly fast and powerful, it bothered me endlessly that Barbarik couldn’t demonstrate that it wasn’t a truly uniform sampler. This eventually lead to the development of ScalBarbarik.

The Birth of ScalBarbarik

Since CMSGen passed all the tests of Barbarik, we had to come up with a new trick to distinguish it from truly uniform samplers. ScalBarbarik‘s (PDF) underlying system is still the same as Barbarik: we take a CNF, take 2 samples from it, and blow both of these samples up to a certain number. However, how we blow them up is where the trick lies. Before, they were both blown up the same way into solutions that are equally easy/hard to find. However, this time around, we’ll make one of the solution types much harder to find than the other. For this, we’ll use Vegard Nossum’s SHA-1 CNF generator (PDF) to force the system to reverse a partial, reduced-round SHA-1 hash, with some fixed inputs & outputs. This allows us to both change the complexity of the problem and the number of solutions to it rather easily.

While one set of solutions will be hard to find, the other ones will be trivial to find — if one special variable is set to TRUE, the finding a set of solutions is trivial But when it’s set to FALSE, the system has to reverse a reduce-round SHA-1. The logic behind this is that the uniform-like systems will likely be finding the easy solutions with much higher probability than the hard solutions, so they will sample much more unevenly. Indeed that’s the case:

Note that as the hardness parameter is increased, CMSGen is rejected more and more often, and eventually it’s rejected for all CNFs. Also interesting to note is that QuickSampler and STS get both rejected, as before, but this time around, STS gets rejected for all 50 CNFs, rather than for only 36 out of 50. In other words, ScalBarbarik is overall a stronger/better distinguisher.

Conclusions

With the birth of Barbarik, a set of uniform-like testers were shown to be less than ideal, and a new, more robust near-uniform sampler was born, CMSGen. But as a the gauntlet has been throw down by CMSGen, a new tool emerged, ScalBarbarik, to help find the non-truly uniform samplers. With this cycle in mind, I hope that new, more elaborate, and higher-quality uniform-like samplers will emerge that will be able to beat ScalBarbarik at its own game, improving the quality of the sampling while maintaining the speed advantage that uniform-like samplers enjoy over truly uniform samplers. With better uniform-like sampling tools, hopefully we’ll be able to make headway in automated test case generation (imagine having it as part of all development IDEs), higher performance function synthesis, and hopefully even more diverse areas of interest for the general public.

How Approximate Model Counting Works

SAT, SMT, ,

Approximate model counting allows to count the number of solutions (or “models”) to propositional satisfiability problems. This problem seems trivial at first given a propositional solver that can find a single solution: find one solution, ban it, ask for another one, ban it, etc. until all solutions are counted. The issue is that sometimes, the number of solutions is 2^50 and so counting this way is too slow. There are about 2^266 atoms in the universe, so counting anywhere near that is impossible using this method.

Exact Counting

Since we cannot count 1-by-1, we are then left with trying to count in some smarter way. There are a bunch of methods to count exactly, the simplest is to cut the problem on a variable, count when the variable is True, count when the variable is False, recursively, and add them all up. Given caching of components that recur while “cutting” away, this can be quite successful, as implemented by sharpSAT (see Marc Thurley’s paper).

These counters can scale quite well, but have some downsides. In particular, when the memory runs out, the cache needs to be groomed, sometimes resorting back to 1-by-1 counting, which we know will fail as there is no way 2^200 can be counted 1-by-1 in any reasonable amount of time. The caching systems used are smart, though, retaining last-used entries when the cache needs to be groomed. However, sometimes this grooming algorithm can lead to cyclic behaviour that effectively simulates 1-by-1 counting.

Approximate Counting

What Chakraborty, Meel and Vardi did in their paper, was to create a counter that counts not exactly, but “probably approximately correctly”. This jumble of terms basically means: there is a certain probability that the counting is correct, within a given threshold. We can both improve the probability and the threshold given more CPU time spent. In practical terms, the probability can be set to be over 99.99% and the threshold can be set to be under 20%, still beating exact counters. Note that 20% is not so much, as e.g. 2^60*1.2 = 2^(60.3).

A Galton Box

So what’s the trick? How can we approximately count and give guarantees about the count? The trick is in fact quite simple. Let’s say you have to count balls, and there are thousands of them. One way to do it is to count 1-by-1. But, if you have a machine that can approximately half the number of balls you have, it can be done a lot faster: you half the balls, then check if you have at least 5 doing 1-by-1 counting. If you do, you half them again, and check if you have at least 5, etc. Eventually, let’s say you halved it 11 times and now you are left with 3 balls. So approximately, you must have had 3*2^11 = 6144 balls to begin with. In the end you had to execute the 1-by-1 count only 11*5+3+1 =59 times — a lot less than 6144! This is the idea used by ApproxMC.

Approximately Halving Using XORs

The “approximate halving” function used by ApproxMC is the plain XOR function, populated with variables picked with 50% probability. So for example if we have variables v1…v10, we pick each variable with 50% probability and add them into the same XOR. Let’s say we picked v1,v2,v5 and v8. The XOR would then be: v1⊕v2⊕v5⊕v8=1. This XOR is satisfied if an odd number of variables from the set {v1,v2,v5,v8} are 1. This intuitively forbids about half the solutions. The “intuitively” part of course is not enough, and if you read the original paper you will find the rigorous mathematical proof for the approximate halving of solutions this XOR function provides.

OK, so all we need to do is add these XORs to our original problem and we are done! This sounds easy, but there is a small hurdle and there is a big hurdle associated with this.

The small hurdle is that the original problem is a CNF, i.e. a conjunction of disjunctions, looking like “(v1 OR v2) AND (v2 OR not v3 OR not v4) AND…”. The XOR obviously does not look like this. The straightforward translation of XOR into CNF is exponential, so we need to add some variables to cut them smaller. It’s not that hard to figure this out and eventually add all the XORs into the CNF.

XORs, CDCL, and Gauss-Jordan Elimination

The larger hurdle is that once the XORs are in the CNF using the translation, the CNF becomes exponentially hard to solve using standard CDCL as used in most SAT solvers. This is because Gauss-Jordan elimination is exponentially hard for the standard CDCL to perform — but we need Gauss-Jordan elimination because the XORs will interact with each other, as we expect there to be many of them. Without being able to resolve the XORs with each other efficiently and derive information from them, it will be practically impossible to solve the CNF.

The solution is to tightly integrate Gauss-Jordan elimination into the solving process. CryptoMiniSat was the first solver to do this tight integration (albeit only for Gaussian elimination, which is sufficient). Other solvers have followed, in particular the work by Tero Laitinen and work by Cheng-Shen Han and Jie-Hong Roland Jiang. CryptoMiniSat currently uses the code by Han and Jiang after some cleanup and updates.

The latest work on ApproxMC and CryptoMiniSat has added one more thing besides the tight integration of the CDCL cycle: it now allows in- and pre-processing to occur while the XORs are inside the system. This brought some serious speedups as pre- and inprocessing are important factors in SAT solving. In fact, all modern SAT solvers strongly depend on them being active and working.

Concluding Remarks

We have gone from what model counting is, through how approximate counting works from a high-level perspective, all the way to the detail of running such a system inside a modern SAT solver. In case you want to try it out, you can do it by downloading the pre-built binaries or building it from source.

SMT Competition’14 and STP

Development, SAT, SMT, , ,

The 2014 SMT competition‘s QF_BV divison is over (benchmark tarball here), and the results are (copied from here):

Solver Errors Solved Not Solved CPU time (solved instances)
Boolector 0 2361 127 138077.59
STP-CryptoMiniSat4 0 2283 205 190660.82
[MathSAT] 0 2199 289 262349.39
[Z3] 0 2180 308 214087.66
CVC4 0 2166 322 87954.62
4Simp 0 2121 367 187966.86
SONOLAR 0 2026 462 174134.49
Yices2 0 1770 718 159991.55
abziz_min_features 9 2155 324 134385.22
abziz_all_features 9 2093 386 122540.04

First, let me congratulate Boolector by Armin Biere. STP came a not-so-close second. STP was meant to be submitted twice, once with MiniSat and once with CyrptoMiniSat4 — this is the only reason why the STP submission is called STP-CryptoMiniSat4. Unfortunately, the other submission could not be made because of some compilation problems.

About the results

There are a couple of things I would like to draw your attention to. First is the cumulated solving time of solved instances. Note how it decreases compared to MathSat and Z3. Note also the differences in the DIFF of the number of solved instances. It’s relatively small between 4Simp…MathSat(<40) and increases dramatically with STP and Boolector (with around 80 each). Another thing of interest is that STP is surrounded by commercial products: Boolector, Z3 and MathSAT are all products you have to pay for to use in a commercial setting. In contrast, the biggest issue with STP is that if the optional(!) CryptoMiniSat4 is linked in, it's LGPLv2 instead of MIT licensed. In other words, a lot of effort is in there, and it's all free. Sometimes free as in beer, sometimes free as in freedom.

About STP

Lately, a lot of work has been done on STP. If you look a the github repository, it has about 80 issues resolved, about 40 open, lots of pull requests, and a lot of commits. A group of people, namely (in nickname order): Dan Liew, Vijay Ganesh, Khoo Yit Phang, Ryan Govostes, Trevor Hansen, a lot of external contributors (e.g. Stephen McCamant) and myself have been working on it pretty intensively. It now has a an automated test facility and a robust build system besides all the code cleanup and other improvements.

It’s a great team and I’m happy to be a minor part of it. If you feel like you could contribute, don’t hesitate to fork the repo, make some changes, and ask for a pull request. The discussions on the pull requests can be pretty elaborate which makes for a nice learning experience for all involved. Come and join — next year hopefully we’ll win :)