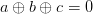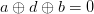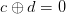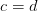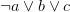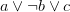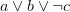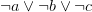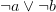Category Archives: SAT

Dreaming up a parallel SAT architecture

SAT,

When someone looks at the speed of solving when using parallel SAT solvers, it is easy to see that scaling doesn’t really work — especially for the hard UNSAT problems. In the past months I have been struggling to think of an architecture that will enable me to write a SAT solver that solves this problem. Let me share with you where I got. It will be more of a brainstorming than a descriptive blog post, but maybe it will help you avoid pitfalls, or maybe just to get a better picture of parallel SAT solving.

The constraints:

  • Clauses must be shared… all the time. Not “when it’s good enough” as per ManySat — that architecture doesn’t work well for UNSAT problems. The performance of a fully shared scheme should be able to overtake a ManySat-like architecture with ease. Only sharing low-glue or high-activity clauses does not work. This is easy to test: write a single-threaded SAT solver with high-glue learnt clause detaching on backtracking. It will work decidedly worse, even though you would clean those clauses anyway when doing clause cleaning. The reason? I don’t know… probably we need those clauses in our current local (=var activities similar) search.
  • Clauses need to have glues and activities. Glues could be dynamically updated, but the gain is not that much and the burden is a bit too much — so make that static. Activities (which are inherently dynamic) are important though (see CryptoMiniSat), and they must be lock-free as they would need to be updated frequently.
  • Memory is scarce when implication caching is used. Implication cache must be shared and updated across the parallel solvers. This not only lowers memory usage, but is an important way to share information other than clauses.
  • Parallel solvers must be lean otherwise the burden of programming a correct solver would be far too much
  • Simplifications must be carried out regularly, which needs the coordinated stopping / interruption of all parallel solvers

My architectural solution:

  • Make a lean class that only handles: clause attachment, detachment and propagation. I will need to add on-the-fly hyper-binary resolution and on-the-fly useless binary clause removal as well, as those are tightly coupled to propagation
  • Make a class that handles search&conflict generation. This class has the lean class as parent. This generates conflict clauses and has its own variable & clause activities. The class checks for new conflict clauses form other solvers after every conflict it generates, and attaches those clauses when that doesn’t need trail-rewriting — though this latter could be made optional. This class does not store a list of clauses. The tricky part of this class is on-the-fly subsumption. We will handle that by not shortening the clause but instead adding a new one and detaching the old one. The thread-coordindating class will handle the propagation of this update to all other threads. Checks for interruption are done after every generated conflict.
  • A thread-coordinating class that handles clause storage, clause distribution, and simplification. This class stops all threads if UNSAT or SAT is found by one thread, and interrupts them if clause-cleaning needs to be carried out. This class also has the lean class as parent, since e.g. clause vivification or variable-replacement need propagation.

Data structures:

  • Fully shared clauses. No move-to-front strategy, instead literal-sorting is carried out once in a while (during simplification I would assume). This has already been implemented, and is only about 10% slower than non-shared clauses in single-threaded mode.
  • Interrupt handler. This is just a flag set by the coordinating solver. The subsolvers check this flag after every conflict generated, and either exit (if SAT/UNSAT is found) or just stop and mark each learnt clause locked (if cleaning the learnt clause database)
  • Implication cache. Needs read-write lock, as most of the time it will be read to do on-the-fly self-subsuming resolution with non-existent binary clauses. Can only have literals added, not removed. Removal and updating of literals is performed only during simplification. Updating (i.e. writing) is done by threads only when doing propagation at decision level 1.
  • Distribution of newly learnt clauses. A ‘lock-free’ (how I don’t like this — it’s misleading, it has locks) datastructure for each thread in the thread-coordinating class that allows the storage of a pre-fixed number of clauses, accessible & writeable without locks until the buffer is filled (at which point we lock & update pointers).

Dilemmas:

  • Maybe thread-management while searching (i.e. learnt clause cleaning and sharing) should be a different class from the one that performs simplification. The former would not need to have propagation at all. Separation of duties always leads to cleaner code.
  • Single-threaded solving is now only an afterthought, and it would be interesting to see how the solver performs in single-threaded mode. I hope it will be only slightly worse than if it didn’t have this architecture around it. It is interesting to note, though, that the structure of the solver will be much cleaner than huge-blob single-threaded solvers tend to be.
  • OpenMP will probably not suffice, as read-write locks are not available, and implication cache sharing is a very important part of the architecture. Fully locking that datastructure when using it would incur too much overhead — most (99.9%) of the time we will be reading it. This means the code might not be as portable as I wished it would be. I think the read-write lock is the only thing I am missing to implement all of this using OpenMP.

Notes:

  • This architecture lets the designer easily change the propagation mechanism. Just re-write the lean class. I have actually done that, and I can have both move-to-front (does not work with sharing) and static clause propagation strategies. People could write their own with ease.
  • Conflict generation&search class should have an object pointer passed to it that is an instance of a class that has a abstract search class as its parent. We could then change restart settings on-the-fly by passing different object pointers.
  • We could save state (i.e. stop&restart search) easily by interrupting all threads and saving the clause database (+learnt clause cleaning state). Simplifications should be fully stateless, so no state would need to be saved for those.

Okay, this is as far as I got. I have the lean class and the search&conflict generation class, the shared clause architecture, and the stateless simplifications ready, but the coordinating class is currently highly entangled with the conflict generation class, so those need to be separated. Further, I want to fix on-the-fly subsumption because it seems to be an easy way to improve the efficiency of conflict generation: if we can shorten a non-learnt clause at every 10th conflict, that is essentially a surely good conflict clause that will never be cleaned. The effect of not having to clear clauses is important when e.g. 6x more conflicts (for a 6-core CPU) are being generated per second than with a single-threaded solver.

Understanding Implication Graphs

SAT, , ,

Having won the SAT Race with CryptoMiniSat, I think I can now confess that I still don’t understand conflict generation. So today, I sat down and I tried to understand it. The result is some fun code, a lot of reading, and great pictures. Let me share with you these auto-generated graphs — the generator will be released with CMSat 3.0.0, so you will be able to generate them, too. These graphs show something called an ‘implication graph’, which is nothing more than a graphical way to show how propagations were made by the reasoning engine. For instance, if variable x1 and x2 are both FALSE, then clause ‘x1 V x2 V x3’ will force x3 to be TRUE to satisfy the clause. Okay, so much for talk, let’s see the graphs!

Our first implication graph had a clause “-70 55 42” (light green box) that caused a conflict — that is to say, somehow the variable setting {x70=TRUE, x55=FALSE, x42=FALSE} was set, the SAT solver realised that this is wrong, and something has to be done. Let’s look at what lead here! Guesses are coloured orange here, so it seems we made the following guesses during our SAT solving: x71=TRUE, x73 = FALSE, x42=FALSE. Now, we could just say, oh, well, setting x73 to FALSE was a dumb idea, just reverse that guess, and be done with it. That’s the easy (and the fast) way, but we are less lazy than that and we want to understand the reasons. So we do something called the conflict analysis to find something called an asserting clause that will not only let us reverse the guess x73=FALSE, but will also give the SAT solver a reason why that is a necessary assignment given its previous guesses and their consequences.

Consequences in the graph are coloured dark green, and there are exactly 3 of them: x70=TRUE, x55=FALSE and x56=TRUE. Each of these is a consequence of a clause that is in the SAT solver, marked on the edge(s) leading to it. For example, x56 is set to TRUE, because of the guess x73=FALSE and the clause “x56 V x73” marked on the edge leading to x56. A consequence that has one edge leading to it was propagated by a 2-long clause, a consequence that has 2 edges leading to it was propagated by a 3-long clause (e.g. consequence “x70=TRUE”, propagated by “x70 V x55 V x73”), etc. Okay, so how do we get to the reason? Well, we start out with the conflict, the clause “-x70 V x55 V x42” (at the bottom), and we do resolutions with this clause, going bottom up. We do as many resolutions as needed to reach the first UIP (also called “articulation vertex” or “dominator”), which is a unique point on the graph through which all paths go through from the highest decision level guess, in this case x73=FALSE, at decision level 56 (noted with a @56). If you take a look, the paths from x73=FALSE diverge from the very first point onwards, and there is no single point where they converge again. This means that the (first and only) dominator will be x73=FALSE itself, and we have to resolve with all clauses on the path:

  1. Start with clause “-x70 V x55 V x42”
  2. Resolve with clause “x70 V x55 V x73”
  3. Resolve with clause “-x55 V-x56 V -x71”
  4. Resolve with clause “x56 V x73”

This list is noted on the bottommost box’s lowest entry. When we resolve with these clauses, we are actually doing cuts on the graph, like this:

My drawing capabilities aren’t exactly great, but you can see that the cuts are successively higher and higher, until we reach the cut that has on its outer part the literals -x73, x71 and -x42. Unsurprisingly, exactly the inverse of these literals are what make up the final conflict clause. Now, if we unroll the implications until decision level 47 (but not the guess x42=FALSE), then with this clause added, variable x73 will propagate to TRUE automatically, essentially reversing the wrong guess — but also giving a reason why it needs to be reversed.

If you enjoyed the previous graph, here is another to entertain you further:

And its corresponding, not too obvious solution:

Note that I was too lazy to draw cuts 10, 11 and 12 around the assignment x145=FALSE (at decision level 39). The UIP in this case is again at the decision variable, x164. If you are still interested, here are some other examples:

PS: Thanks to George Katsirelos for his help understanding this (disclaimer: all faults belong to me alone).

Presentation at Hackito Ergo Sum

SAT, , , , ,

The HES’11 event was great: I had the pleasure of listening to some awesome presentations, and to meet some great people. The most interesting presentation from a non-technical point of view was the attacks at the automount feature of Linux, which everybody thinks is completely secure, but is in fact very flawed due to some buggy rendering libraries. It’s quite interesting that almost everyone thinks that their Linux installation is secure, when in fact if Linux was mainstream, viruses would be abound — but Linux is only a minor player, so malicious software is rarely written for it.

My presentation is available here. I tried mostly to demonstrate how SAT solvers work as an element of the technique that can most amply described as:

As the graphics show, the SAT solver is in fact only one player in this environment. As it turns out, it is the very last step after obtaining the cipher, creating equations describing the cipher, and converting the ANF equations into CNF. The best way to create equations from the original cipher is to use the excellent Sage Maths library for this, a tutorial of which is here. Then, the ANF created by Sage can be transcribed into CNF using, e.g. the anf2cnf tool by Martin Albrecht and me. Finally, the CNF must be solved with a SAT solver to recover the key of the cipher. This last step can be carried out by many SAT solvers, such as lingeling or MiniSat, but I prefer CryptoMiniSat, since I am the main developer for that SAT solver, and it is also very convenient to use in this domain due to some domain-specific advantages it has over other solvers. The middle two steps of the diagram are all automated by the Grain-of-Salt tool if you don’t want to use Sage, and it also contains some example ciphers, so you don’t even have to do step no. 1 in case you wish to work on one of multiple pre-defined industrial ciphers.

In case you are interested in the visualisations I used during my presentation, here is the set of tools I used. For the 3D visualisation, I used 3Dvis by Carsten Sinz — it’s a great tool to extract some structure from problems already in CNF. In case you still have the ANF, it contains more structure, though, and so it is more interesting to look at it that way. Unfortunately, that is rarely the case for typical SAT problems, and so one must often resort back to 3Dvis. For the example search tree, I used CryptoMiniSat 1.0 and gnuplot, and for the example real-time search, I used CryptoMiniSat 2.9.0, available from the same place. Unfortunately, CryptoMiniSat 2.9.0 cannot generate a search tree yet, but this eventually will be included, with time — especially if you join the effort of developing the solver. We are always looking forward to people joining in and helping out with various issues from graph generation to algorithm performance tuning, or even just some fun research.

Come to Hackito Ergo Sum’11

SAT, ,

There is going to be a nice hacker conference in Paris real soon now: Hackito Ergo Sum, between the 7th and the 11th of April. There will be plenty of interesting talks, among them, I will also be presenting some fun crypto-breaking :) The schedule is here, I am scheduled for the first day, on Thursday at 11:30 AM. If you are in or near Paris, come around for the conference, I am sure it will be a really nice one :) If you are interested in meeting me, we can also meet in Paris, just drop me a mail, but better yet, come and chat with me at the conf, I will be there all day long.

The HES conference mainly focuses on attacks: against software, crypto, infrastructure, hardware, and the like. If you are interested what the current trend in attacking these systems is, and/or you are interested in making your organisation safer from these attacks, it’s a good idea to come and visit to get the hang of what’s happening. It’s also a great opportunity to meet all the organisations and people who are driving the change in making software and hardware systems more secure by demonstrating their weaknesses and presenting possibilities for securing them.

Meet you at HES’11 ;)

Recovering XORs from a CNF

SAT

Let’s suppose you are looking to recover XORs. It’s fun to recover XORs, because you could try to XOR the XORs together to obtain new information, like this:

a \oplus b \oplus c = 0
a \oplus d \oplus b = 0
therefore,
c \oplus d = 0
therefore,
c = d

Simple XOR recovery

The simplest way to recover an XOR clause is to look for clauses that encode it, which is the following set of clauses:

\neg a \vee b \vee c
a \vee \neg b \vee c
a \vee b \vee \neg c
\neg a \vee \neg b \vee \neg c

Finding such a set is not that hard: we need to first sort each clause according to its literals, then sort the list of clauses according to their sizes and variable contents and then go through the list of clauses linearly. If you think through the first two steps, you will see that it ensures that the above 4 clauses are next to each other in the list of clauses, making it trivial to find them.

Improved XOR recovery

There is only one small glitch with the algorithm above: other sets of clauses can also make up XORs. For example, this set of clauses:
\neg a \vee b \vee c
a \vee \neg b \vee c
a \vee b \vee \neg c
\neg a \vee \neg b

Notice that all I took away was one literal from one clause. Now, if a CNF implies \neg a \vee \neg b it must surely also imply \neg a \vee \neg b \vee \neg c since this latter one is less stringent than the first one. So, we could easily have it inside our CNF, but we don’t for reasons of lazyness: who wants to keep around data that is implied by unit propagation already? However, keeping in mind that the second, less stringent clause is implied by the first one is important: it could lead to the discovery of more XORs.

Results

Let’s move on to the magical territory of practical SAT solving. Let’s first take a typically industrial problem, UTI-20-10p0:

$./cryptominisat_old UTI-20-10p0.cnf
[...]
c Finding non-binary XORs:     0.10 s (found:       0, avg size: -nan)

The old, 2.9.0 CryptoMiniSat seems to have no luck at finding any XOR clauses. This is very typical: industrial instances seem not to contain any XOR clauses at all. Let’s look at the new algorithm now:

$./cryptominisat_new UTI-20-10p0.cnf
[...]
c XOR finding finished. Num XORs:   9288

All right, that seems better.

Edited to add: Thanks to Vegard Nossum for telling me something was odd with XOR recovery. As usually is the case, answering a question is much easier than knowing what question to ask.

Edited to add2: The above algorithm can be easily improved by using cached literals and stamping.