Category Archives: SAT

How to use CryptoMiniSat 2.9 as a library

Development, SAT,

There have been some questions asked about how to use CryptoMiniSat as a library. Here, I give a simple example usage to help any future potential users. If there are any question that seems unanswered, please feel free to add them as a comment to this post.

First, we initialize the solver with high verbosity:

#include "cmsat/Solver.h"
using namespace CMSat;

SolverConf conf;
conf.verbosity = 2;
Solver solver(conf);

Then we add the variables 0..9:

for(int i = 0; i < 10; i++) {
  solver.newVar();
}

And add a clause that would look in the DIMACS input format as "2 -5 10 0":

vec clause;
clause.push(Lit(1, false));
clause.push(Lit(4, true));
clause.push(Lit(9, false));
solver.addClause(clause);

We now create the assumptions that would look in DIMACS input format as "1 0" and "-5 0":

vec assumps;
assumps.push(Lit(0, false));
assumps.push(Lit(4, true));

We now solve with these assumptions:

lbool ret = solver.solve(assumps);

Let's see if the state of the solver after solving is UNSAT regardless of the assumptions:

if (!solver.okay()) {
  printf("UNSAT!\n");
  exit(0);
}

Note that okay() can only be FALSE if "ret" was "l_False". However, it is important to distinguish between two kinds of l_False: one where only the assumptions couldn't be satisfied, and one where no matter what the assumptions are, the problem is unsatisfiable. See below for more.

Now let's check that the solution is UNSAT relative to the assumptions we have given. In this case, let's print the conflicting clause:

if (ret == l_False) {
  printf("Conflict clause expressed in terms of the assumptions:\n");
  for(unsigned i = 0; i != solver.conflict.size(); i++) {
    printf("%s%d ", (solver.conflict[i].sign()) ? "" : "-", solver.conflict[i].var()+1);
  }
  printf("0\n");
}

The above will print an empty clause if solver.okay() is FALSE.

Now, let's see if the solution is SAT, and if so, print the solution to console, using DIMACS notation:

if (ret == l_True) {
  printf("We have the solution, it's here: \n");
  for (unsigned var = 0; var != solve.nVars(); var++)
    if (S.model[var] != l_Undef) {
      printf("%s%d ", (solver.model[var] == l_True)? "" : "-", var+1);
      printf("0\n");
    }
}

If solver.okay() is still TRUE (which it must be, if the ret was l_True), we can now add new clauses and new variables without restriction, and solve again (potentially with different assumptions). Note that most of the above applies to MiniSat as well.

When compiling the code, you have to pass the parameters such as:

$ g++ -fopenmp -lcryptominisat myprogram.cpp -o myprogram

PS: Thanks go to Martin Albrecht for pointing out some ambiguities in my explanation of the library usage, which have now been fixed.

On hyper-binary resolution

Research, SAT, ,

Hyper-binary resolution is actually quite straightforward, or at least appears to be. Let’s take the following example. The clauses in our database are the following:

-a V b
-a V c
-b V -c V g
-b V -c V d
-d V g

Let’s set a to true, and see what happens. Immediately, b and c get set to true through binary clauses. If we now propagate g through the clause -b V -c V g, we ought to do hyper-binary resolution straight away, and add the clause -a V g — some call this lazy hyper-binary resolution. Good, one more binary clause!

But then… So now we have nothing to propagate using only binary clauses, we have to propagate using a long clause, -b V -c V d. As good citizens, we also do (lazy) hyper-binary resolution, coming up with the clause -a V d. Good, one more binary clause! One slight glitch now… d propagates to g, using a binary clause. But this means that setting a can propagate to g without -a V g, the first hyper-binary clause we added! So the first hyper-binary clause we added is in fact useless, it needs to be removed. If we applied transitive reduction, it would remove the first hyper-binary clause -a V g automatically.

Let’s go a bit deeper here. How could we have avoided adding the first hyper-binary clause? The obvious answer is: we should have started with -b V -c V d instead of -b V -c V g. But how easy would have it been to know (i.e. calculate) that starting with that different long clause would have made our work easier? I am not sure it would have been easy to know. And of course the example above is very trivial. It could be made much-much more complicated: g could have been reached with any number of hyper-binary resolutions from d — so simple binary look-ahead would not have helped.

I am stuck here. Any ideas?

Thoughts on SAT@home

SAT, ,

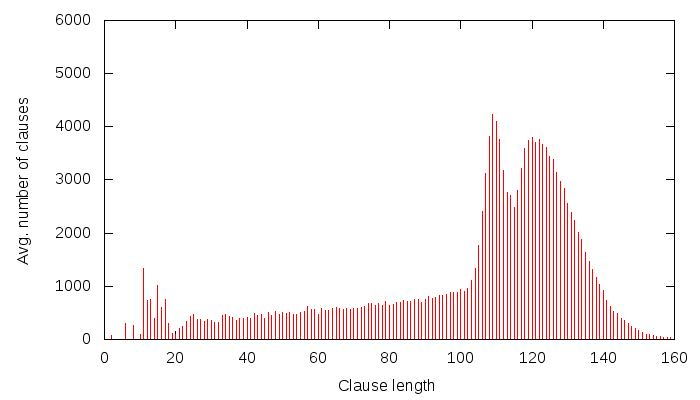
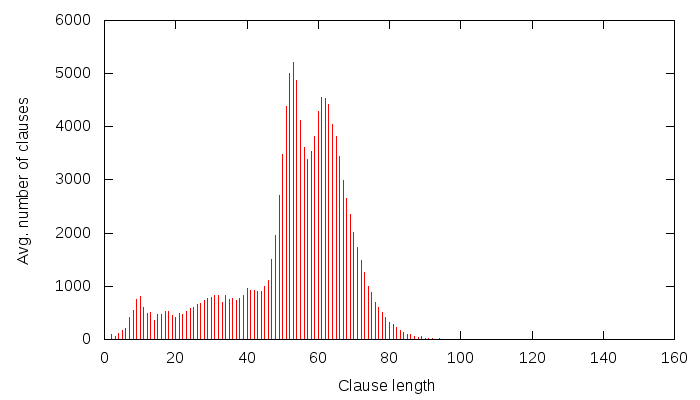
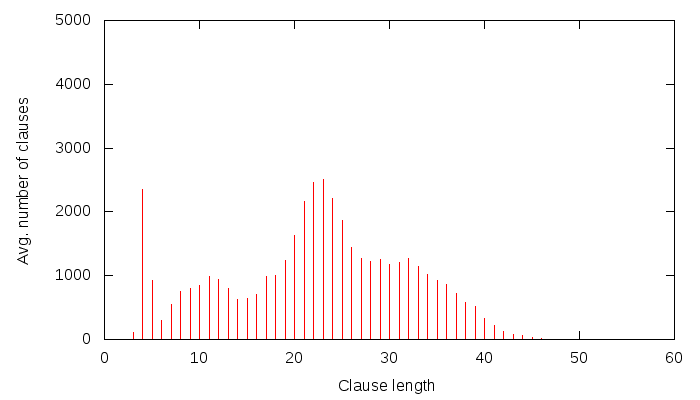
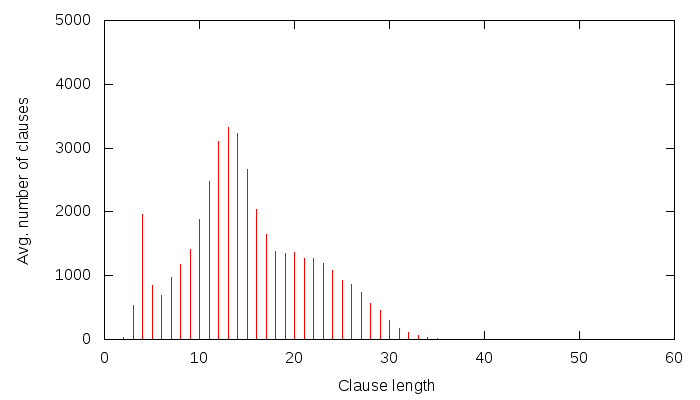
If you have ever wondered how your multi-month SAT problem could be solved, the answer is here: SAT@home by some kind Russian researchers! This idea has been brewing in my head, we even started a mini-project with a  friendly American researcher, but we never got it into a working condition :(. It’s great that someone took the time to do it, though. Creating such a setup has some easier and harder parts. Setting up a BOINC server is not that hard, but it needs to run 24/7, which is difficult, unless you are department head at a university or you have a company behind you. Then the scripts need to be written, which is relatively easy to do, but testing and debugging is time-consuming. The really hard part, though, is how to distribute the workload. Treatises could be written on that, and the one above uses the simplest method, that of cutting up the problem along a couple of variables. It’s a good start, I think: starting easy is always the best way to start — the first automobile didn’t try to achieve 300km/h speeds, and it didn’t have to.

In the long run, I guess the setups will get more and more complicated, combining many techniques from cutting on variables, to clause sharing with a multitude of clause usefulness heuristics, to sharing parameter usefulness statistics. Workshares themselves could eventually be diversified, some doing ‘simple’ search without resolution, some doing only resolution (and clause cleaning?), some doing only (specific) simplification algorithms such as subsumption or strengthening, some doing data analysis on the current state of the problem such as reachability analysis, number of gates or other higher-level elements such as adders in the problem, etc. In other words, there are many ways to improve this. Maybe even a common interface to such a system could be laid down where different SAT solvers could be plugged in and used without notice.

A friend of mine has once written me a mail describing his work, which essentially talks about paying for a webpage not by looking at adverts, but by running a javascript program. The idea is, of course, that we could write a SAT solver in javascript, and make people run the script by putting it on a well-visited webpage. The server would then distribute SAT problems to the javascripts, which would send some computed data back (like learnt clauses), while the person is surfing the page. Cheap (maybe even free) and essentially unlimited CPU time for hard problems. We could use it to answer some fun math questions, or break some cryptographic systems, for example… just have to find someone crazy enough to write a SAT solver in javascript! :)

Failed literal probing and UIP

SAT, , ,

I have just realised that CryptoMiniSat, having won a number of medals, does one of the most basic things, failed literal probing, all wrong. Let me tell you why it’s all wrong. In essence, failed literal probing is trivial. We enqueue a fact, such as a, and then propagate it. If this fails, i.e. if two opposing facts such as g and -g are derived, we know that a cannot be true, so we set -a. Easy. Or maybe not so easy.

The devil is in the details, so let’s see how we derived both g and -g from a. Let’s assume that we have the following set of binary clauses:
-a V b
-b V c
-b V d
-d V e
-d V f
-e V g
-f V -g

which, from the point of view of a is best described as the graph:

Propagating "a", deriving both "g" and "-g"

The problem is, that if we only derive -a from this graph, we end up with only that one literal set, because -a doesn’t propagate anything on the clauses. This is quite sad, because, in fact, we could derive something stronger. From the graph it is evident that setting d would have failed: the graph would simply have its upper part cut away completely, but the lower part, including the derivation of both g and -g would still stand:

Deriving both "g" and "-g" from "d"

What is special about node d? Well, it’s where the 1st UIP, the first unique implication point, lies. And it is quite simple to see that -d is in fact the strongest thing we can derive from this graph. It’s much stronger than simply -a, because setting -d propagates on the clauses, giving -b,-a, setting three variables instead of one, including -a. An interesting observation is the following: deriving -b is the 2nd UIP, and deriving -a is the last UIP. In other words, at least in this most simple case, 1st UIP is in fact the strongest, and 2nd, 3rd.. last UIP are less strong in strict order.

Let me remark on one more thing about failed literal probing. Once failed literal probing has been done on literal x and it visited the node set N, there is no need to try to do failed literal probing on any nodes in N, since they cannot possibly fail. Although the failing of a literal can have consequences on the failing of other literals, if we ignore this side-effect, we could speed up failed literal probing by marking literals already visited, and only carrying out failed literal probing on ones that haven’t been marked. This is really trivial, but I haven’t been using it :S

I am quite sure that some advanced SAT solvers (such as lingeling) do all of the above things right. It’s probably only CryptoMiniSat that fails miserably :)

Note: there is a subtle bug with marking literals visited as “OK”. If two different subgraphs could fail, but we abort on the first one, then we might mark a literal OK when in fact it isn’t. It is therefore easiest not to mark any literals if the probe failed (which is very rare).

Note to self: higher level autarkies

Research, SAT, , ,

While reading this thesis, I have had a thought about autarkies. Let me first define what an autarky in SAT solving is:

A partial assignment phi is called a weak autarky for F if “phi*F is a subset of F” holds, while phi is an autarky for F if phi is a weak autarky for all sub-clause-sets F' of F. (Handbook of Satisfiability, p. 355)

What does this mean? Well, it means that in the clause-set {x V y, x} the assignment y=False is a weak autarky, because assigning y to False will lead to a clause that is already in the clause set (the clause x), while the assignment of x=True is a (normal) autarky, because it will satisfy all clauses that x is in. The point of autarkies is that we can remove clauses from the clause set by assigning values to a set of variables, while not changing the (un)satisfiability property of the original problem. In other words, autarkies are a cheap way of reducing the problem size. The only problem is that it seems to be relatively expensive to search for them, so conflict-driven SAT solvers don’t normally search for them (but, some lookahead solvers such as march by Marijn Heule do).

So, what is the idea? Well, I think we can have autarkies for equivalent literals, too. Here is an example CNF:

 a V d V -f
-b V d V -f
-a V e
 b V e

setting a = -b will not change the satisfiability of the problem.

We can add any number of clause pairs of the form X V Y where Y is any set of literals not in {a, -a, b, -b}, and X is (-)a in clause 1 and (-)b in clause 2. Further, one of the two variables, say, a can be in any clauses at will (in any literal form), though variable b can then only be in clauses defined by the clause pairs. Example:

 a V  d V -f
-b V  d V -f
-a V  e
 b V  e
 a V  c V -h
 a V -f

An extension that is pretty simple from here, is that we can even have clauses whose Y part is somewhat different: some literals can be missing, though again in a controlled way. For example:

 a V d
-b V d V -f
-a V e
 b V e

is possible. It would restrict b a bit more than necessary, but if a is the only one of the pairs missing literals, we are still OK I believe.

Finally, let me give an example of what these higher-level autarkies are capable of. Let’s assume we have the clause set:

 a V  d
-b V  d V -f
-a V  e
 b V  e
 a V  c V -h
 a V -f
 a V  b V  f V -g

setting a=-b now simplifies this to:

 a V  d
-a V  e
 a V  c V -h
 a V -f

which is equisatisfiable to the first one. Further, if the latter is satisfiable, computing the satisfying solution to the former given a solution to the latter is trivial.